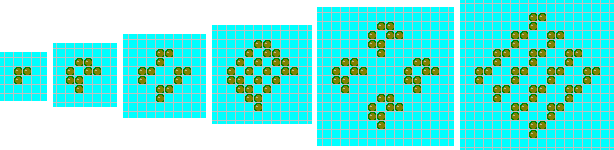
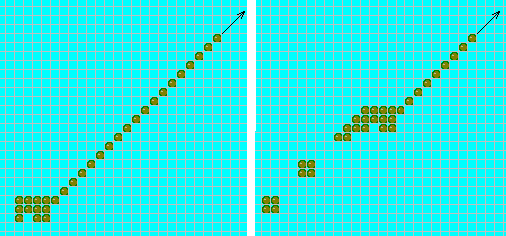
Рис.11. Размножение тримино.
| Мартин Гарднер. Игра Жизнь > |
Предисловие Игра "Жизнь". Часть I Ответы Дополнения Игра "Жизнь". Часть II Игра "Жизнь". Часть III Литература | Вернуться |
Теория клеточных автоматов берет свое начало с середины пятидесятых годов, когда Джон фон Нейман поставил перед собой задачу доказать возможность существования самовоспроизводящихся автоматов. Если такую машину снабдить надлежащими инструкциями, она построит точную копию самой себя, В свою очередь обе эти машины смогут построить еще две; четыре машины построят восемь и т. д. (Это распространение самовоспроизводящихся автоматов является темой захватывающего романа Лорда Дансени "Последняя революция", написанного в 1951 г.). Нейман впервые доказал возможность существования таких машин с помощью "кинематических" моделей машины, способной передвигаться по складу запасных частей, отбирать необходимые детали и собирать новые машины, как две капли воды похожие на нее. Позднее, воспользовавшись идеей, высказанной его другом С. Уламом, фон Нейман дал более изящное и абстрактное доказательство возможности существования самовоспроизводящихся машин.
В новом доказательстве Неймана существенно использовалось понятие "однородного клеточного пространства", эквивалентного шахматной доске бесконечных размеров. Каждая клетка такого пространства может находиться в любом, но конечном числе "состояний", в том числе и в состоянии покоя (называемом пустым, или нулевым, состоянием). На состояние любой клетки оказывает воздействие конечное число соседних клеток. Во времени эти состояния пространства изменяются дискретно, в соответствии с некоторыми "правилами перехода", которые необходимо применять ко всем клеткам. Клетки соответствуют основным частям автомата с конечным числом состояний, а конфигурация из "живых" клеток — идеализированной модели такого автомата. Именно в таком клеточном пространстве и развертывается действие придуманной Конуэем игры "Жизнь". Соседними для каждой клетки в "Жизни" считаются 8 непосредственно окружающих ее клеток. Каждая клетка может находиться в двух состояниях (либо на ней стоит фишка, либо она пуста). При этом правила перехода определяются генетическими законами Конуэя — рождением, гибелью и выживанием фишек, о которых я рассказал в предыдущей главе. Применяя правила перехода к пространству, каждая клетка (или ячейка) которого могла находиться в 29 состояниях и имела 4 соседние клетки (примыкающие к данной по вертикали и горизонтали), Нейман доказал существование самовоспроизводящейся конфигурации, состоящей примерно из 200 000 клеток.
Причина столь чудовищных размеров конфигурации объяснялась тем, что Нейман намеревался применить свое доказательство к реальным автоматам и специально подобрал клеточное пространство, способное имитировать машину Тьюринга — идеальный автомат, названный так в честь его изобретателя, английского математика А. М. Тьюринга, и способный производить любые вычисления. "Погрузив" универсальную машину Тьюринга в созданную им конфигурацию, Нейман получил возможность создать "универсальный конструктор", способный построить любую конфигурацию в пустых клетках пространства, в том числе и точную копию самого себя. За время, прошедшее после смерти Неймана (последовавшей в 1957 г.), предложенное им доказательство существования самовоспроизводящейся системы (речь идет именно о "чистом" доказательстве существования, а не о построении используемой в доказательстве Неймана конфигурации) удалось значительно упростить. Рекордным по простоте явилось доказательство, найденное выпускником инженерного факультета Массачусетского технологического института Э. Р. Бэнксом. В нем используются ячейки, которые могут находиться лишь в четырех состояниях.
Самовоспроизведения в тривиальном смысле — без использования конфигураций, включающих в себя машину Тьюринга,- добиться легко. Удивительно простой пример "тривиальной" самовоспроизводящейся системы предложил примерно в 1960 г. Э. Фридкин, также из Массачусетского технологического института. В этой системе ячейки могут находиться лишь в двух состояниях, причем любая из них, как и в примере Неймана, имеет четырех соседей, а правила перехода сводятся к следующему. Каждая клетка, имеющая в момент времени t четное число (0, 2, 4) живых соседей, в момент времени t + 1 становится пустой (т. е. переходит в нулевое состояние или, если она уже находилась в нулевом состоянии, остается в нем). Каждая клетка, имеющая в момент времени t нечетное число (1, 3) соседей, в момент времени t +1 становится живой (т. е. переходит в ненулевое состояние или сохраняет его, если она уже в нем находилась). Нетрудно показать, что через 2n ходов (число n зависит от выбора конфигурации) любая исходная конфигурация живых клеток воспроизведет себя четыре раза: одна копия расположится справа, другая — слева, третья — сверху, четвертая — снизу от того (уже пустого) места, где находилась начальная конфигурация. Все четыре копии заимствуют 2n клеток у исчезнувшего организма-оригинала. Новая конфигурация через 2n шагов снова размножится (с коэффициентом воспроизводства, равным 4) и т. д. При этом число копий увеличивается в геометрической прогрессии 1, 4, 16, 64, .... На рис. 11 показаны два цикла размножения тримино в форме прямого угла. В 1967 г, Т. Виноград, тогдашний студент Массачусетского технологического института, в своей курсовой работе обобщил правила Фридкина на любое число соседей, а также на произвольную схему примыкания соседних клеток и на любое число измерений (результаты Винограда относятся к клеткам, число состояний которых характеризуется простыми числами).

Множество автоматов такого рода, отличающихся друг от друга схемой примыкания соседних клеток, числом состояний и правилами перехода, исследовал С. Улам. В опубликованной им (совместно с Р. Г. Шрандтом) в 1967 г. статье "О рекурсивно определенных геометрических объектах и схемах роста" Улам описал несколько различных игр. На рис. 12 показано 46-е поколение организма, родившегося из одной-единственной фишки, стоявшей на центральной клетке. Как и в игре Конуэя, клетки в игре Улама могут находиться в двух состояниях, однако соседними считаются клетки, примыкающие к данной лишь по вертикали и по горизонтали, но не по диагонали ("соседи" в представлении Неймана). Рождение фишки происходит на клетке, имеющей одного и только одного соседа, а все клетки n-го поколения погибают после рождения (n + 2)-го поколения. Иначе говоря, на любом этапе эволюции выживают лишь два последних поколения. На рис. 12 темными изображены новорожденные клетки — общее число их составляет 444. Светлые клетки предыдущего поколения — их 404 — исчезнут на следующем ходу. Обратите внимание на характерную деталь конфигурации, которую Улам назвал "обглоданной костью".

Улам проводил эксперименты и с такими играми, в которых две конфигурации могли расти до тех пор, пока они не сталкивались. В следовавшей за столкновением "битве" одной стороне иногда удавалось одержать верх над другой, в других же случаях обе армии исчезали. Улам рассмотрел также игры на трехмерных досках — кубических "мозаиках", заполняющих все пространство. Основные результаты собраны в его статьях, опубликованных в сборнике "Очерки теории клеточных автоматов".
Аналогичные игры можно вести и на бесконечных досках, клетки которых имеют форму равносторонних треугольников и правильных шестиугольников. Несмотря на сильное внешнее отличие, по существу эти игры не вносят в анализ ничего нового, и с помощью подходящего определения "соседних" клеток их всегда можно свести к эквивалентным играм на обычной доске с клетками в форме квадратов. Соседними могут быть не только клетки, имеющие общие стороны или вершины. Например, в шахматах для клетки, на которой стоит конь, соседними (т. е. влияющими на ее состояние) считаются все клетки, на которые можно пойти конем или на которых стоят угрожающие ему фигуры. Как заметил А. Беркс, такие игры, как шахматы, шашки и го, допустимо рассматривать как клеточные автоматы со сложными окрестностями каждой клетки (окрестностью называется совокупность соседей) и правилами перехода. Противники, делая очередной ход, выбирают среди множества допустимых состояний то, которое должно привести их к определенному конечному состоянию — выигрышу.
Среди наиболее значительных вкладов в теорию клеточных автоматов самую громкую известность получил предложенный Э. Ф. Муром способ доказательства существования конфигураций, которые Дж. У. Тьюки назвал "садами Эдема". Эти конфигурации не могут возникать в процессе игры, поскольку никакая предшествующая конфигурация отличного от них типа не может их породить. "Сады Эдема" должны быть заданы с самого начала — в нулевом поколении. Поскольку конфигурации такого типа не имеют "предшественников", они не могут быть самовоспроизводящимися. Подробно метод Мура изложен в его популярной статье "Математика в биологических науках", опубликованной в Scientific American (September 1964). Более строгое изложение этого метода приведено в уже упоминавшемся сборнике под редакцией А. Беркса.
Алви Р. Смит, специалист по теории клеточных автоматов из Нью-Йоркского университета, обнаружил простой способ, позволяющий применять метод Мура к игре Конуэя. Рассмотрим два квадрата размером 5Х5 клеток. У одного из них все клетки свободны, а на центральном поле другого стоит одна фишка. Поскольку уже на следующем ходе 9 центральных клеток обоих квадратов обязательно должны оказаться идентичными (в данном случае все эти клетки будут просто пустыми), про такие квадраты обычно говорят, что они "взаимно уничтожаемы". Из теоремы Мура следует, что конфигурация типа "сад Эдема" должна возникать в игре Конуэя. К сожалению, доказательство этой теоремы ничего не говорит о том, как найти "сады Эдема", и они до сих пор не обнаружены. Конфигурация типа "сад Эдема" может оказаться и простой, и чрезвычайно сложной. С помощью одной из выведенных Муром формул Смит сумел доказать, что такую конфигурацию всегда можно заключить в квадрат со стороной в 10 миллиардов клеток, но и этот результат ненамного облегчает поиски указанной конфигурации.
Сам Смит работает над созданием клеточных автоматов, имитирующих машины для распознавания образов. Хотя сегодня такая проблема может показаться имеющей лишь чисто теоретический интерес, вполне возможно, что наступит время, когда органам зрения роботов потребуется своего рода "сетчатая оболочка" для распознавания образов. Скорости современных сканирующих устройств весьма малы по сравнению со скоростью "параллельных вычислений", которую обеспечивает сетчатка глаз животных, передающая в их мозг одновременно тысячи различных сигналов. Параллельный режим работы представляет собой фактически единственную возможность значительно повысить быстродействие современных вычислительных машин, поскольку без параллельного функционирования их быстродействие ограничено сверху предельной скоростью распространения электромагнитных сигналов в схемах миниатюризации, а именно, скоростью света. Обложка февральского номера журнала Scientific American за 1971 г., воспроизведенная на рис. 13, хорошо иллюстрирует возможности предложенной Смитом простой процедуры, с помощью которой параллельный режим работы используется в конечном одномерном клеточном пространстве для распознавания симметрии палиндромов. Каждая клетка при этом обладает некоторым множеством состояний (число их зависит от количества различных символов, которые могут появиться в структуре палиндрома), а соседними по отношению к данной клетке оказываются лишь две клетки, лежащие по разные стороны от нее.

Смит символически представляет палиндром "ТОО НОТ ТО HOOT" ("Слишком жарко, чтобы улюлюкать" — англ.) с помощью клеток, расположенных в верхнем ряду чертежа. При этом каждая клетка всей диаграммы может оказаться в четырех различных состояниях: буквы Т, О и Н представляются, соответственно, голубым, красным и желтым цветом, а черный цвет обозначает начало и конец палиндрома. Белые клетки в нижних рядах — это состояния покоя, или пустые клетки. Горизонтальные ряды клеток, располагающиеся под исходным рядом, характеризуют собой структуру последующих поколений, возникающих в процессе эволюции верхней конфигурации (для дискретных временных шагов) при условии выполнения определенных правил перехода. Другими словами, данный рисунок представляет собой пространственно-временную диаграмму эволюции верхнего ряда клеток, где каждый последующий ряд клеток характеризует следующее поколение в процессе превращений начальной конфигурации.
При первом переходе каждый цвет на нашей схеме сдвигается на одну клетку влево и на одну клетку вправо, за исключением концевых оттенков, которые блокируются черным цветом; при этом на очередном шаге эволюции черные клетки могут смещаться только по направлению внутрь конфигурации. Каждая клетка, с которой контактируют два цвета, переходит в новое состояние, которое символически обозначается путем деления клетки на четыре одинаковых треугольника. При этом левый треугольник окрашивается в цвет, который на предыдущем этапе располагался слева, а на правый треугольник переходит цвет, располагавшийся ранее справа. Результат, получившийся после первого хода, показан на клетках второго ряда.
Отметим также, что если соседняя пара клеток образует на своей границе (в центре) наклонный квадрат, целиком закрашенный одинаково, это указывает на "столкновение" одинаковых цветов и символически обозначается двумя черными точками, которые ставятся в верхнем и нижнем белых треугольниках, оставшихся в левой клетке. Черные точки в указанной клетке сохраняются и во всех последующих поколениях, пока справа, в непосредственном соседстве от этой клетки вновь не произойдет столкновение различных цветов — тогда черные точки в клетке стираются. В случае, когда имеет место столкновение различных цветов, точки в левой клетке пары не возникают во всех последующих поколениях, даже если справа от нее на более поздних этапах сталкиваются два одинаковых цвета.
При каждом ходе соответствующие оттенки перемещаются на одну клетку влево или вправо (в направлении, которое указывают закрашенные треугольники того же цвета) и, в соответствии с описанными выше правилами, вся процедура повторяется вновь. Если палиндром состоит из n букв, где n — четное, как в нашем примере (в случае нечетного n описанная схема слегка видоизменяется), то легко убедиться, что после n/2 ходов сохраняются лишь две соседние клетки, находящиеся в "возбужденном" состоянии. Если в левой клетке этой пары оказываются черные точки, то, следовательно, автомат распознал палиндромный характер первоначального ряда клеток (букв). В центре диаграммы можно видеть, как "сталкиваются" пары одинаковых оттенков в том же самом порядке, как они идут в исходном палиндроме в направлении от центра к левому и правому его концам. Как только распознавание произошло, левая клетка последней пары стирается, а правая клетка переходит в состояние "да", символически обозначенное здесь зеленым квадратом, вложенным в соответствующую клетку. Если же черные точки в левой клетке отсутствуют, то это будет служить признаком того, что исходная конфигурация не является палиндромом. В этом случае левая клетка становится пустой, а правая переходит в состояние "нет".
Машине Тьюринга, которая производит вычисления последовательно, для распознавания палиндрома длины n требуется, вообще говоря, n2 шагов. В нашем случае, хотя распознавание имеет место на шаге n/2, клетки в состоянии "да" на диаграмме в последующих поколениях постепенно сдвигаются вправо, что символизирует переход состояния "да" от клетки к клетке по направлению к внешней границе клеточного пространства. Конечно, не представляет большого труда разработать более эффективные устройства для распознавания палиндромов с использованием реальной электронной аппаратуры, однако в данном случае проблема состоит в том, чтобы проделать это в совершенно абстрактном одномерном клеточном пространстве, в котором информация может передаваться только от данной клетки к соседним клеткам, причем в самом начале нам не известен даже центр первоначальной последовательности символов. Как заключает Смит, переходя на чисто бытовые сравнения, после первого шага каждая из трех клеток с точками "пытается вообразить", будто как раз она находится в центре палиндрома. В то же время крайние клетки с точками на следующем шаге "испытывают горькое разочарование" вследствие столкновения различных цветов с их правой стороны. Поэтому клетка с точками, лежащая в центре, может узнать, что она действительно располагается в центре палиндрома только в n/2 поколении.
А теперь несколько слов о поразительных результатах, полученных при анализе игры Конуэя. Сам Конуэй был прекрасно осведомлен об опыте своих предшественников при разработке такого рода игр. Поэтому он, учтя все их достоинства и недостатки, при выборе своих рекурсивных правил (генетических законов) постарался прежде всего избежать двух крайностей: слишком большого числа конфигураций с быстрым и неограниченным ростом, а также слишком большого числа конфигураций, которые быстро исчезают. Приняв во внимание все эти факторы, он сумел разработать игру, отличающуюся удивительной степенью непредсказуемости и порождающую такие замечательные объекты, как пульсирующие конфигурации и мчащиеся космические корабли. Как я уже отмечал, в свое время Конуэй высказал предположение о том, что не существует ни одной исходной конфигурации, состоящей из конечного числа фишек, которая могла бы беспредельно расти (по числу фишек), пообещав награду тому, кто либо докажет, либо опровергнет это предположение.
В ноябре 1970 г. Конуэю пришлось выдать обещанную премию группе математиков из Массачусетского технологического института, занимавшейся проблемами искусственного интеллекта. В эту группу входили Р. Эйприл, М. Билер, Р. У. Госпер, Р. Хауэлл, Р. Шроппель и М. Спесинер. С помощью разработанной Спесинером программы для вывода на экран дисплея ЭВМ последовательных этапов эволюции различных конфигураций Госпер сделал поистине поразительное открытие: он обнаружил "ружье", стреляющее "глайдерами"! На рис. 14 изображена конфигурация, которая превращается в такое "ружье". На сороковом ходу из "ружья" вылетает первый "глайдер", через каждые 30 ходов — следующий "глайдер" и так до бесконечности. С появлением каждого "глайдера" число фишек на доске увеличивается на 5, в результате чего происходит неограниченный рост популяции.

"Глайдерное ружье" позволило его создателям совершить много других замечательных открытий. На серии распечаток (присланных мне Р. Т. Уэйнрайтом из Йорктаун Хайте, шт. Нью-Йорк), которые представлены на рис. 15, показано столкновение 13 "глайдеров". Рассыпавшись на части, они превращаются... в "глайдерное ружье"! На последней схеме "глайдерное ружье" ведет огонь, выстреливая один "глайдер" за другим.
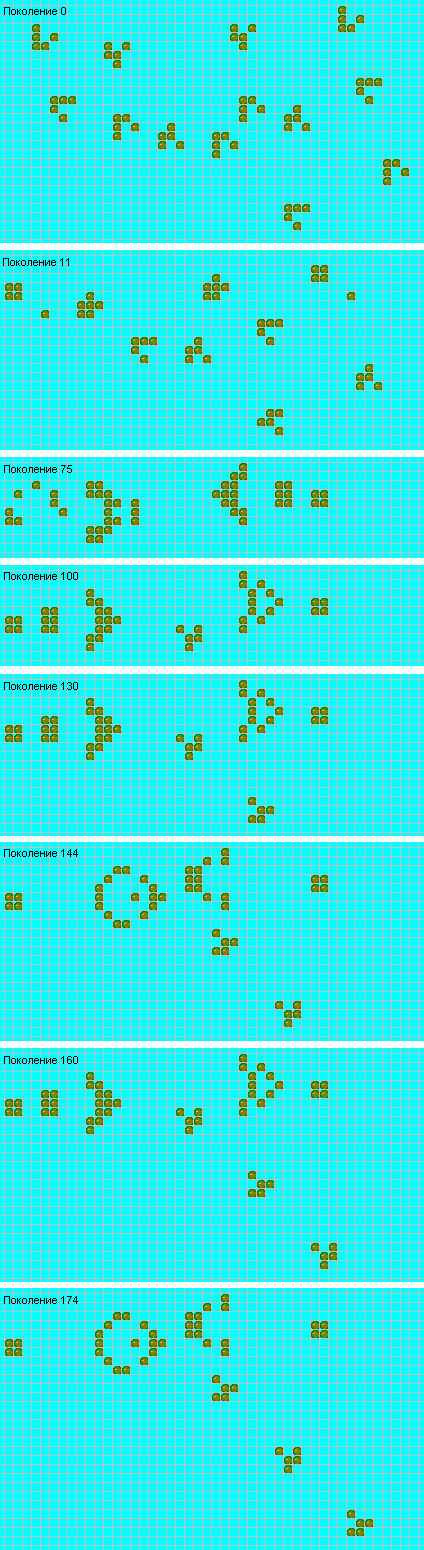
Та же группа исследователей обнаружила "пентадекатлон" (рис. 16),- пульсирующую конфигурацию с периодом, равным 15, способную "поглотить" любой сталкивающийся с ней "глайдер".

"Пентадекатлон" может также отражать "глайдер", изменяя курс последнего на 180°. Расположив друг против друга два "пентадекатлона", можно провести между ними "теннисный матч": они будут перекидывать "глайдер" как теннисный мячик. Совершенно неожиданные результаты возникают при рассмотрении пересекающихся потоков "глайдеров": появляющиеся вновь конфигурации могут быть самыми причудливыми и в свою очередь испускать "глайдеры". Иногда конфигурация, образующаяся при пересечении потоков "глайдеров", начинает расти и, расширяясь, поглощает все "ружья". В других случаях осколки, вылетающие из области, в которой происходит пересечение потоков, могут вывести из строя одно или несколько "ружей". Последнее достижение группы из Массачусетского технологического института, убедительно свидетельствующее об их виртуозности,- хитроумная комбинация из восьми "ружей". В пересечении создаваемых ими потоков "глайдеров" возникает целый "завод" "космических кораблей" среднего типа, а каждые 300 ходов происходит даже "запуск" такого "корабля"!
Создание "глайдерных ружей" открывает удивительную возможность, используя игру Конуэя, смоделировать машину Тьюринга — универсальную вычислительную машину, способную (по крайней мере, в принципе) производить все те действия, которые только доступны самым совершенным из современных ЭВМ. Идея заключается в том, чтобы использовать "глайдеры" в качестве единичных импульсов для хранения и передачи информации, а также для выполнения необходимых логических операций, допускаемых схемными элементами реальных вычислительных машин. Если с помощью игры Конуэя окажется возможным создать машину Тьюринга, то сразу же встает вопрос о создании универсального конструктора, позволяющего создавать такие машины, которые могли бы полностью копировать и воспроизводить самих себя. До сих пор никому не удалось "построить" машину Тьюринга в пространстве, клетки которого могут находиться лишь в двух состояниях, а "соседство" клеток понимается по Конуэю (т. е. они должны иметь либо общую сторону, либо общую вершину). Вместе с тем, ранее было доказано, что в пространстве, все клетки которого могут находиться в двух состояниях, а "близость" клеток понимается по Нейману, построить машину Тьюринга невозможно.
Группа ученых из Массачусетса открыла много других периодически изменяющихся конфигураций (рис. 17). Одна из них, получившая название "палка", имеет период, равный 2, и представляет собой одну из разновидностей "флип-флопов". При этом ее можно как угодно растягивать, а каждое из двух ее состояний является зеркальным отражением другого.
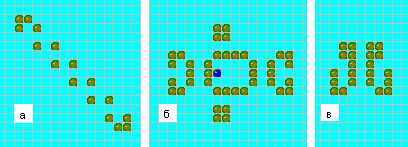
Вторая конфигурация была еще раньше открыта Конуэем — это так называемый "осциллятор Герца". После каждых четырех ходов синяя точка перемещается к противоположной стороне внутренней рамки, в результате чего вся фигура "осциллирует" с периодом, равным 8. Третья конфигурация, которую обнаружил Дж. Д. Коллинс из Маклина, шт. Вайоминг, называется "опрокидыватель", потому что каждые 7 ходов у нее меняются местами верх и низ.
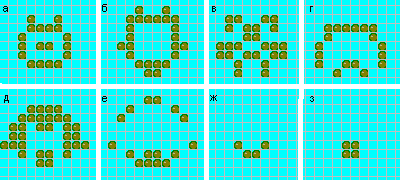
"Чеширского кота" (рис. 18) открыл К. Р. Томпкинс из Короны, шт. Калифорния. На шестом ходе (ж) от кота остается лишь "улыбка", а "морда" совершенно исчезает. Следующим ходом "улыбка" тоже уничтожается, и лишь неизменный "блок" (з) — отпечаток кошачьей лапы — напоминает о том, что некогда на этом месте находился кот. "Жнейка", изображенная на рис. 19, была "построена" Д. У. Пойнером из Великобритании. Как видно из рисунка, она движется снизу вверх по бесконечной диагонали со скоростью света, осциллируя с периодом, равным 4, и оставляя за собой вдоль всего пути устойчивые фигуры, символически изображающие снопы. "К сожалению,- пишет изобретатель "жнейки",- мне не удалось создать "сеятеля" — движущуюся фигуру, которая могла бы засевать поле с той же скоростью, с которой жнейка его убирает".
Р. Уэйнрайт, о котором я упоминал выше, также является автором многих любопытных исследований. Например, разместив случайным образом 4800 фишек в клетках квадрата размером 120 X 120 (с плотностью фишек, равной 1/3), он проследил их эволюцию на протяжении 450 поколений. Плотность этого "первичного студня", как называет его Уэйнрайт, сильно уменьшилась и стала равняться всего лишь 1/6. Исчезнут ли все фишки в конце концов или же они будут, как утверждает исследователь, продолжать "просачиваться" из поколения в поколение с некоторой минимальной постоянной плотностью — ответ на этот вопрос пока не известен. Во всяком случае, на протяжении 450 поколений удалось проследить появление 42 "короткоживущих" "глайдеров". Уэйнрайту удалось обнаружить также 14 конфигураций, которые после первого хода превращаются в один или несколько "глайдеров". Больше всего "глайдеров" (а именно, 14) получается из фигуры, показанной на рис. 20, а. Конфигурация в форме буквы Z, найденная Коллинсом и Дж. Ландом из Пиуоки, шт. Висконсин (рис. 20, б), после 12 ходов превращается в два "глайдера", которые разлетаются в противоположных направлениях. Тот же Уэйнрайт установил, что если два "глайдера" следуют наперерез друг другу так, как это показано на рис. 20, в, то после четвертого хода все фишки с доски исчезают. Наконец, если два "легких космических корабля" движутся опасным курсом, ведущим к их столкновению (рис. 20, г), то после седьмого хода доска оказывается абсолютно пустой, как и в случае столкновения двух "глайдеров". (Этот факт установил У. У. Вагнер из Анахейма, шт. Калифорния.)

Уэйнрайт, кроме того, экспериментировал с разными бесконечными полями, заполняя их правильными устойчивыми фигурами. Такие конфигурации он назвал агарами. Если, например, в агар, изображенный на рис. 21, поместить один-единственный "вирус" (т. е. одну фишку), причем так, чтобы он касался вершин четырех "блоков", то агар уничтожит "вирус", а через два хода восстановит свой прежний вид. Если же "вирус" поместить в клетку так, как это показано на рисунке (или же в любую из семи других клеток, симметрично расположенных вокруг "блоков"), то начнется неизбежное разрушение агара. "Вирус" постепенно поглотит внутри агара все активные участки, оставив на поле пустую двусторонне симметричную область, несколько напоминающую овал. Ее граница будет непрерывно расширяться во все стороны со "скоростью света", причем не исключено, что это расширение будет происходить бесконечно долго.

Наиболее практичным приложением теории клеточных автоматов, как считает Бэнкс, являются, по-видимому, вопросы разработки электронных цепей, способных к самовосстановлению, а также проектирования различных специальных типов электронного оборудования. Правда, сегодня нам трудно говорить о том, насколько существенной в итоге может оказаться эта теория для развития физики и биологии. Возможно, она играет важную роль в процессах роста зародышевых клеток, при создании идентичных копий молекул ДНК, в работе нервных сетей, в генетических изменениях развивающихся популяций и т. д. Наконец, нетрудно проследить глубокую аналогию между этой теорией и процессами развития жизни. Если "первичный бульон", состоящий из различных аминокислот, имеет достаточно большую протяженность и, кроме того, если мы располагаем определенным запасом времени, то в результате действия сложных правил перехода, присущих самой структуре материи и законам природы, в этой среде может развиться популяция самовоспроизводящихся подвижных автоматов. Можно даже допустить, что наше пространство-время имеет гранулярную структуру, состоящую из отдельных дискретных модулей, а вселенная, по предположениям Фридкина и других исследователей, является огромнейшим клеточным автоматом, управляемым громадным компьютером. Если это предположение справедливо, то привычное нам понятие движения окажется всего лишь некоторой моделью более сложного явления. Точно так же движение космического корабля, рассматриваемое на элементарном микроуровне, вполне может уподобиться движению конфигураций типа "космических кораблей", перемещающихся на макроуровне,- ведь здесь фактически существует лишь некоторое изменение состояний основных клеток пространственно-временного континуума, подчиняющееся правилам перехода, пока еще нам неизвестным.